Предположим, что уравнение ![]() при помощи
некоторых тождественных преобразований приведено к виду
при помощи
некоторых тождественных преобразований приведено к виду ![]() .
.
Заметим, что такое преобразование можно вести разными способами, и при этом
будут получаться разные функции ![]() в правой
части уравнения. Уравнение
в правой
части уравнения. Уравнение ![]() эквивалентно уравнению
эквивалентно уравнению ![]() при любой
функции
при любой
функции ![]() . Таким
образом, можно взять
. Таким
образом, можно взять ![]() и при
этом выбрать функцию (или постоянную)
и при
этом выбрать функцию (или постоянную) ![]() так, чтобы
функция
так, чтобы
функция ![]() удовлетворяла тем свойствам, которые понадобятся нам для обеспечения нахождения
корня уравнения.
удовлетворяла тем свойствам, которые понадобятся нам для обеспечения нахождения
корня уравнения.
Для нахождения корня уравнения ![]() выберем
какое-либо начальное приближение
выберем
какое-либо начальное приближение ![]() (расположенное, по возможности, близко к корню
(расположенное, по возможности, близко к корню ![]() ). Далее будем вычислять последующие приближения
). Далее будем вычислять последующие приближения
Заметим: тот факт, что ![]() --
корень уравнения
--
корень уравнения ![]() , означает,
что
, означает,
что ![]() есть абсцисса точки пересечения графика
есть абсцисса точки пересечения графика ![]() с прямой
с прямой
![]() . Если же при каком-либо
. Если же при каком-либо ![]() вычислено значение
вычислено значение ![]() и взято в
качестве нового аргумента функции, то это означает, что через точку графика
и взято в
качестве нового аргумента функции, то это означает, что через точку графика ![]() проводится
горизонталь до прямой
проводится
горизонталь до прямой ![]() , а оттуда
опускается перпендикуляр на ось
, а оттуда
опускается перпендикуляр на ось ![]() . Там и
будет находиться новый аргумент
. Там и
будет находиться новый аргумент ![]() .
.
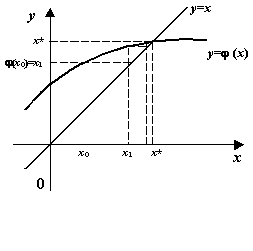
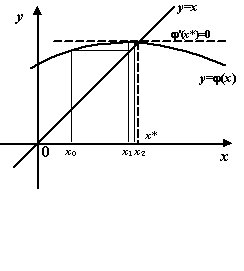
Проследим, как изменяются последовательные приближения ![]() при различных вариантах взаимного расположения графика
при различных вариантах взаимного расположения графика ![]() и прямой
и прямой
![]() .
.
1). График ![]() расположен, по крайней мере в некоторой окрестности корня, включающей начальное
приближение
расположен, по крайней мере в некоторой окрестности корня, включающей начальное
приближение ![]() , в некотором
угле со сторонами, имеющими наклон менее
, в некотором
угле со сторонами, имеющими наклон менее ![]() к
горизонтали (то есть стороны угла -- прямые
к
горизонтали (то есть стороны угла -- прямые ![]() , где
, где
![]() ):
):
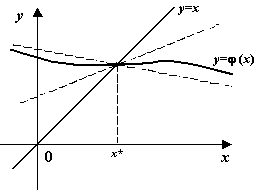
Если предположить вдобавок, что функция ![]() имеет
производную
имеет
производную ![]() , то этот
случай соответствует тому, что выполнено неравенство
, то этот
случай соответствует тому, что выполнено неравенство ![]() , при
, при ![]() , близких к корню
, близких к корню ![]() . Проследим в этом случае за поведением последовательных
приближений
. Проследим в этом случае за поведением последовательных
приближений ![]()
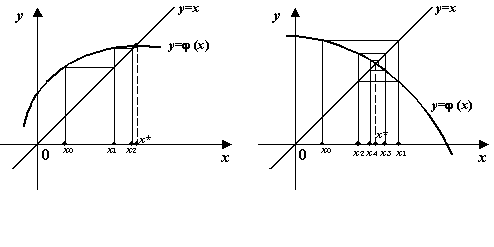
Мы видим, что каждое следующее приближение ![]() будет в этом случае расположено ближе к корню
будет в этом случае расположено ближе к корню ![]() , чем предыдущее приближение
, чем предыдущее приближение ![]() . При этом, если график при
. При этом, если график при ![]() лежит ниже горизонтали
лежит ниже горизонтали ![]() , а при
, а при
![]() -- выше её (что, в случае наличия
производной, верно, если
-- выше её (что, в случае наличия
производной, верно, если ![]() ), то
приближения
), то
приближения ![]() ведут себя
монотонно: если
ведут себя
монотонно: если ![]() , то
последовательность
, то
последовательность ![]() монотонно
возрастает и стремится к
монотонно
возрастает и стремится к ![]() , а если
, а если
![]() , то монотонно убывает и также стремится к
, то монотонно убывает и также стремится к
![]() . Если же график функции
. Если же график функции ![]() лежит выше
горизонтали
лежит выше
горизонтали ![]() при
при ![]() и ниже её при
и ниже её при ![]() (это так, если
(это так, если ![]() ), то
последовательные приближения
), то
последовательные приближения ![]() ведут себя
иначе: они "скачут" вокруг корня
ведут себя
иначе: они "скачут" вокруг корня ![]() , с каждым
скачком приближаясь к нему, но так же стремятся к
, с каждым
скачком приближаясь к нему, но так же стремятся к ![]() при
при ![]() .
.
Заметим, что если функция ![]() не
монотонна в окрестности точки
не
монотонна в окрестности точки ![]() , то
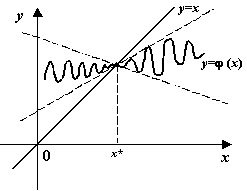
последовательные приближения могут вести себя нерегулярно (то есть не монотонно
и не оказываясь попеременно то левее, то правее корня, а делая скачки
относительно корня при произвольных номерах (см. следующий чертёж):
, то
последовательные приближения могут вести себя нерегулярно (то есть не монотонно
и не оказываясь попеременно то левее, то правее корня, а делая скачки
относительно корня при произвольных номерах (см. следующий чертёж):
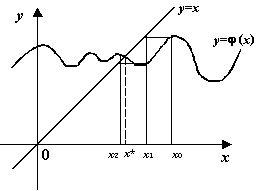
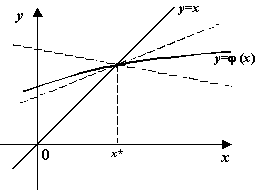
2). График ![]() расположен, по крайней мере в некоторой окрестности корня, вне некоторого угла
со сторонами, имеющими наклон более
расположен, по крайней мере в некоторой окрестности корня, вне некоторого угла
со сторонами, имеющими наклон более ![]() к
горизонтали (то есть стороны угла -- прямые
к
горизонтали (то есть стороны угла -- прямые ![]() , где
, где
![]() ):
):

Если функция ![]() имеет
производную
имеет
производную ![]() , то в этом
случае при
, то в этом
случае при ![]() , близких к
корню
, близких к
корню ![]() , выполнено
неравенство
, выполнено
неравенство ![]() .
.
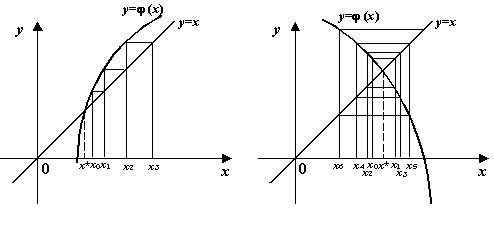
Каждая следующая итерация ![]() будет в
этом случае расположена дальше от корня
будет в
этом случае расположена дальше от корня ![]() , чем предыдущая,
, чем предыдущая, ![]() . При этом,
в зависимости от того, пересекает ли график прямую
. При этом,
в зависимости от того, пересекает ли график прямую ![]() "снизу вверх" или "сверху вниз" (см. рис.), последовательность
"снизу вверх" или "сверху вниз" (см. рис.), последовательность
![]() монотонно удаляется от корня
монотонно удаляется от корня ![]() или же итерации удаляются от
или же итерации удаляются от ![]() , оказываясь попеременно то справа, то слева от корня.
, оказываясь попеременно то справа, то слева от корня.
Ещё одно замечание: если не выполнено ни условие ![]() , ни
условие
, ни
условие ![]() , то
итерации
, то
итерации ![]() могут
зацикливаться. На чертеже ниже приведён пример зацикливания, когда уравнение
имеет вид
могут
зацикливаться. На чертеже ниже приведён пример зацикливания, когда уравнение
имеет вид ![]() .
.
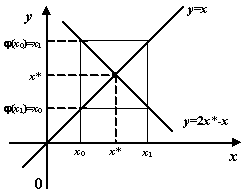
Мы видим, что для сходимости итераций к корню, вообще говоря, не обязательно
наличие производной у функции ![]() . Однако
метод итераций гораздо удобнее формулировать в терминах, связанных со значениями
производной. Именно так мы и сформулируем наши наблюдения в виде теоремы.
. Однако
метод итераций гораздо удобнее формулировать в терминах, связанных со значениями
производной. Именно так мы и сформулируем наши наблюдения в виде теоремы.
При этом скорость сходимости задаётся неравенствами
Доказательство. Пусть ![]() . По формуле конечных приращений,
применённой к отрезку между точками
. По формуле конечных приращений,
применённой к отрезку между точками ![]() и
и ![]() , получаем
, получаем
Неравенство ![]() очевидно,
поскольку из того, что
очевидно,
поскольку из того, что ![]() и
и ![]() лежат в окрестности
лежат в окрестности ![]() длины
длины ![]() , следует,
что
, следует,
что ![]() .
.
Поскольку
Выше мы отмечали, что привести уравнение ![]() к виду
к виду ![]() можно,
выбирая
можно,
выбирая ![]() в виде
в виде ![]() , где
, где ![]() --
произвольная функция. При различных способах выбора
--
произвольная функция. При различных способах выбора ![]() получаются
разные модификации метода итераций, которые имеют отличающиеся свойства: разную
скорость сходимости (но не меньшую той, что гарантирована теоремой) и разную
потребность в вычислении значений функции
получаются
разные модификации метода итераций, которые имеют отличающиеся свойства: разную
скорость сходимости (но не меньшую той, что гарантирована теоремой) и разную
потребность в вычислении значений функции ![]() или
или ![]() , а также их
производных.
, а также их
производных.
Отметим самые употребительные из этих методов.